平时会用到不少的排序模型,但是一直没有系统化总结,今天还是认真总结下,如有错误,求大佬们不吝指出。
1. LR-逻辑回归
逻辑回归通常对输入特征如用户年龄、性别、item属性、描述等进行变换,然后输入到模型中,通常训练目标为是否点击。在推理阶段,将同样的特征输入到模型中,模型预测出点击概率,最终经过排序得到推荐item的列表。
逻辑回归核心为sigmoid函数,wx输入到sigmoid函数中,通常使用梯度下降算法来更新参数w。
逻辑回归的优点:
- 强数学含义支撑。LR属于广义线性模型的一种。
- 可解释性强。从公式层面来看,LR数学形式就是不同特征之间的加权之和,最终过一个sigmoid函数,将输出值限制在0到1之间。根据不同特征的权重,可以明显观察到哪些特征重要。
- 工程实现容易。
逻辑回归的缺点:
- 表示能力不足。
- 无法进行特征交叉,学习高阶特征。
2.POLY2-特征交叉的开始
LR存在无法自动进行特征交叉的问题,最容易想到的是人工构造交叉组合特征。公式如下:
$ POLY2(w,x)=\sum_{j_1=i}^{n-1} \sum_{j_2=j_1+1}^{n} w_{h(j_1,j_2)}x_{j_1}x_{j_2}$
可以看到,该方法对所有特征均进行交叉,并对特征组合赋予权重$ w_{h(j_1,j_2)} $,一定程度解决了特征交叉问题,但是本质上还是对于不同特征加权求和的线性模型。
POLY2缺点:
- 交叉特征容易出现极度稀疏问题。使用one-hot编码类别特征之后,容易出现稀疏特征问题。
- 权重参数由n上升到n2,增加训练复杂度。
3.FM-隐向量特征交叉
FM的主要优点是解决稀疏数据下的特征组合问题。
原始的FM公式为:
$ FM=w_0+\sum_{i=1}^n w_ix_i+\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} w_{ij}x_ix_j$
前两项其实就是一阶加权特征,计算复杂度为O(n),第三项中的权重$w_{ij}$,这儿使用到了矩阵分解,分解为 $ W=V^TV $, vi、vj分别为xi、xj的隐向量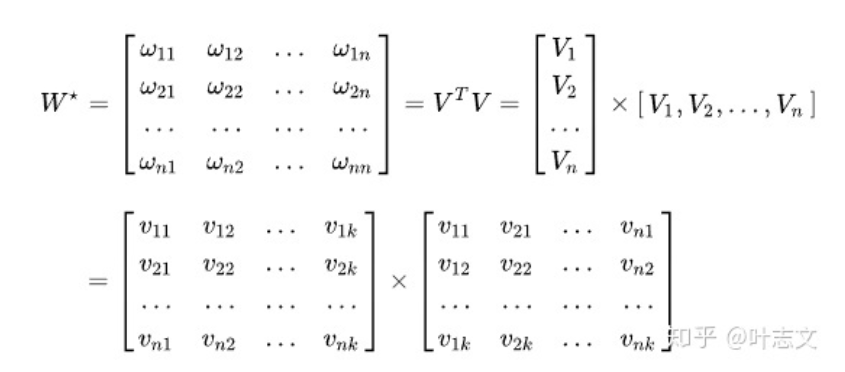
于是,原始公式变为了:
$ FM=w_0+\sum_{i=1}^n w_ix_i+\sum_{i=1}^{n} \sum_{j=i+1}^{n} <v_i,v_j>x_ix_j$
我们假设隐向量的长度为k ,那么交叉项的参数量变为 kn 个。此时时间复杂度仍为O(kn^2),通过以下方式可以简化为O(kn),如下图: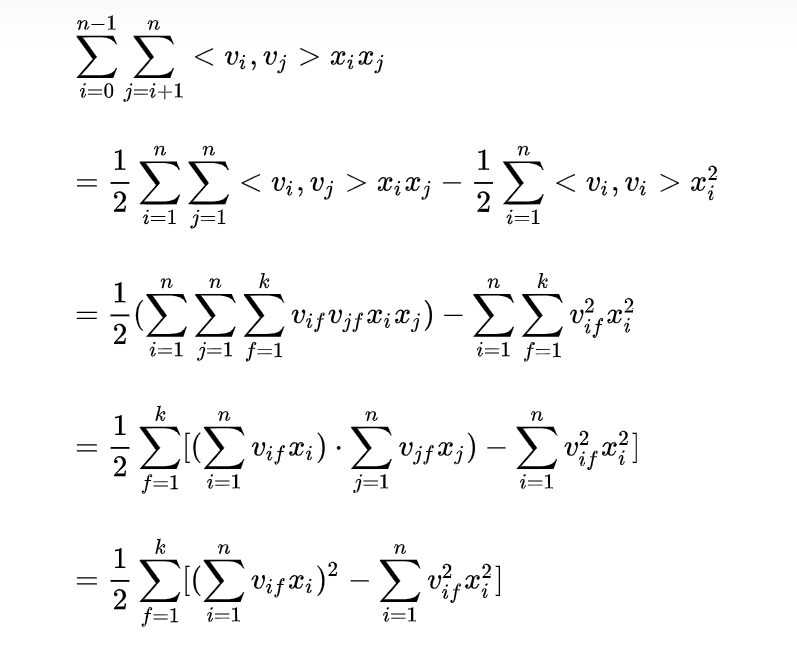
附上核心代码:
import numpy as np |
4.FFM
FFM在FM的基础上进行改进,提出了特征域的概念,特征域里是同一个特征的不同取值。FM做法对于不同特征交叉认为是同等重要的,然而FFM的理论是不同特征的交叉影响不同,举个简单例子。比如有性别、年龄、职业三种特征,那么在与“职业”中的“清洁工”特征交叉时“男性”的隐向量是$v_{男性,职业}$,在与“年龄”中的“中年”特征交叉时,“男性”的隐向量是$v_{男性,年龄}$。这种思维更符合实际场景,不同的特征交叉权重确实应该不同。
FFM使得本来仅取决于特征xi的向量vi还取决于与他交叉的特征xj 所属的特征域 fj,即变成了vifj 。 fj 是第 j 个特征所属的特征域,它有多个特征。
缺点:
- FFM公式无法化简,计算复杂度较高,FFM需要学习n个特征在f个域上的k维隐向量,参数量nfk个,复杂度
$O(kn^2)$
核心代码:import numpy as np
import torch
import torch.nn as nn
class FieldAwareFactorizationMachine(nn.Module):
"""
FFM
"""
def __init__(self, field_dims, embed_dim):
super(FieldAwareFactorizationMachine, self).__init__()
self.offsets = np.array((0, *np.cumsum(field_dims)[:-1]), dtype=np.long)
# 输入的是label coder 用输出为1的embedding来形成linear part
# linear part
self.linear = torch.nn.Embedding(sum(field_dims) + 1, 1)
self.bias = torch.nn.Parameter(torch.zeros((1,)))
# ffm part
print("field_dims", field_dims)
self.num_fields = len(field_dims) # 特征域的数目
self.embeddings = torch.nn.ModuleList([
torch.nn.Embedding(sum(field_dims), embed_dim) for _ in range(self.num_fields)
])
for embedding in self.embeddings:
torch.nn.init.xavier_uniform_(embedding.weight.data)
def forward(self, x):
# bs,fields_num [bs,22]
tmp = x + x.new_tensor(self.offsets).unsqueeze(0)
# linear part forward
## bs,fields_num,1 -> bs,1 [bs,22,1]->[bs,1]
linear_part = torch.sum(self.linear(tmp), dim=1) + self.bias
# ffm part forward
# 为每一个field都使用embedding进行映射编码
# 每个embedding中的shape应该为:bs,filed_num,embedding_num -> bs,22,8
xs = [self.embeddings[i](x) for i in range(self.num_fields)]
ix = []
for i in range(self.num_fields - 1):
for j in range(i + 1, self.num_fields):
# xs[j].shape: torch.Size([2, 22, 8]) bs,field_nums,embedding_num
# xs[j].shape: torch.Size([2, 22, 8])
# xs[j][:, i] shape: torch.Size([2, 8]) bs,embedding_num
ix.append(xs[j][:, i] * xs[i][:, j])
# print("ix len:",len(ix)) 231
# print("ix [0]:",ix[0].shape) #bs,embdding_num -> bs,8
ix = torch.stack(ix, dim=1) # ix: -> bs,231,embedding_num
ffm_part = torch.sum(torch.sum(ix, dim=1), dim=1, keepdim=True) # bs,231,embedding_num -> bs,embedding -> bs,1
x = linear_part + ffm_part
x = torch.sigmoid(x.squeeze(1))
return x
5.DeepFM
顾名思义,DeepFM是Deep与FM结合的产物,
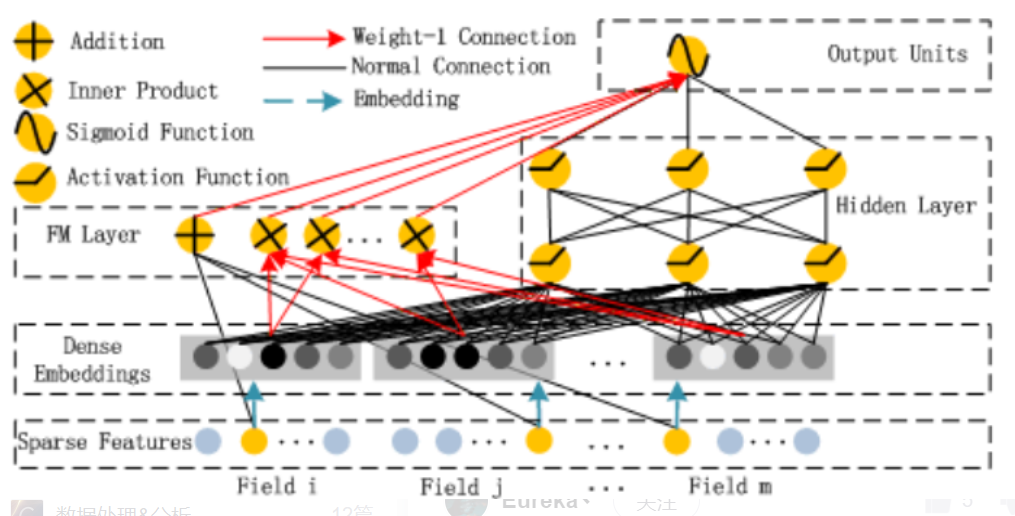
5.1 Sparse Feature
Sparse Feature是指离散型变量。比如现在我有数据:xx公司每个员工的姓名、年龄、岗位、收入的表格,那么年龄和岗位就属于离散型变量,而收入则称为连续型变量。这从字面意思也能够理解。
Sparse Feature框里表示的是将每个特征经过one-hot编码后拼接在一起的稀疏长向量,黄色的点表示某对象在该特征的取值中属于该位置的值。
5.2 Dense Embeddings
该层为嵌入层,用于对高维稀疏的 01 向量做嵌入,得到低维稠密的向量 e (每个01向量对应自己的嵌入层,不同向量的嵌入过程相互独立,如上图所示)。然后将每个稠密向量横向拼接,在拼接上原始的数值特征,然后作为 Deep 与 FM 的输入。
最终输入模型的值如下图,Sparse Feature经过embedding之后,与归一化后的连续特征拼接,一起输入模型
5.3 FM Layer
线性部分 (黑色线段) 是给与每个特征一个权重,然后进行加权和;交叉部分 (红色线段) 是对特征进行两两相乘,然后赋予权重加权求和。然后将两部分结果累加在一起即为 FM Layer 的输出。
5.4 Hidden Layer
Deep 部分的输入 为所有稠密向量的横向拼接,然后经过多层线性映射+非线性转换得到 Hidden Layer 的输出,一般会映射到1维,因为需要与 FM 的结果进行累加。
5.5 Output Units
$ DeepFM=sigmoid(y_{FM}+y_{DNN})$
输出层为 FM Layer 的结果与 Hidden Layer 结果的累加,低阶与高阶特征交互的融合,然后经过 sigmoid 非线性转换,得到预测的概率输出。
优点:
- 两部分联合训练,无需加入人工特征,更易部署;
- 结构简单,复杂度低,两部分共享输入,共享信息,可更精确的训练学习。
缺点:
- 将类别特征对应的稠密向量拼接作为输入,然后对元素进行两两交叉。这样导致模型无法意识到域的概念,FM 与 Deep 两部分都不会考虑到域,属于同一个域的元素应该对应同样的计算。
最后上核心代码:
import numpy as np |
6.DCN
DCN是一个可以同时高效学习低维特征交叉和高维非线性特征的深度模型,不需要人工特征工程的同时需要的计算资源非常低。
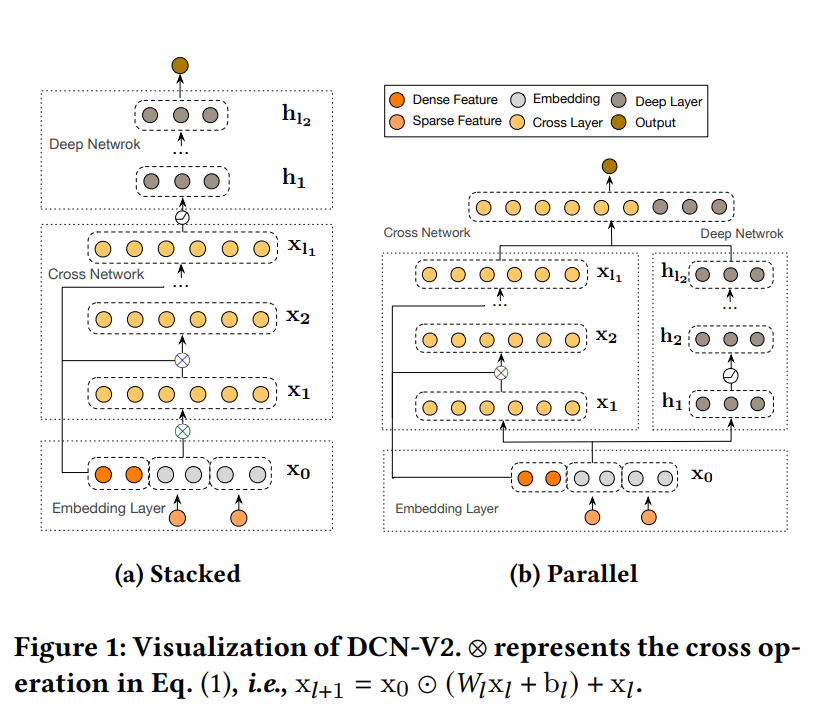
DCN的模型结构图如下,其实模型结构已经较为详细说明了特征的交叉、运行过程。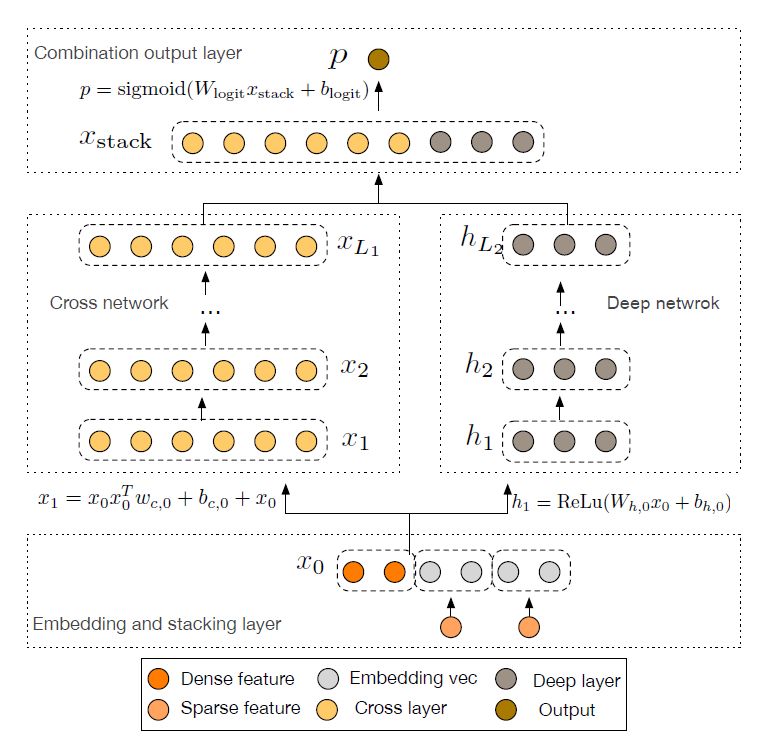
6.1 Embedding Layer
输入的特征分为dense特征和sparse特征。对于sparse特征,通常使用one-hot等编码方式编码,之后通过embedding层进行映射降维,转为dense特征。最后将dense特征与转换过的sparse特征拼接,即图中的x0.
6.2 Cross Network
在交叉层中,使用图中的公式进行特征交叉,并且叠加L层
w和b是需要学习的参数,cross network为1层的时候,我们可以得到的最高是2维的特征交叉;cross network为2层的时候,我们得到的是最高3维的特征交叉;cross network为3层的时候,我们得到的是最高4维的特征交叉;以此类推。。。
因此cross network以一种参数共享的方式,通过对叠加层数的控制,可以高效地学习出低维的特征交叉组合,避免了人工特征工程。
6.3 Deep Network
为全连接网络,用来学习高维非线性特征交叉组合。
6.4 Combination Output Layer
将cross与deep层输出拼接,然后过一个sigmoid进行CTR预估。
最后上核心代码:import numpy as np
import torch
import torch.nn as nn
class DeepCrossNet(nn.Module):
"""
Deep Cross Network
"""
def __init__(self, feature_fields, embed_dim, num_layers, mlp_dims, dropout):
"""
"""
super(DeepCrossNet, self).__init__()
self.feature_fields = feature_fields
self.offsets = np.array((0, *np.cumsum(feature_fields)[:-1]), dtype = np.long)
# Embedding layer
self.embedding = nn.Embedding(sum(feature_fields)+1, embed_dim)
torch.nn.init.xavier_uniform_(self.embedding.weight.data)
self.embedding_out_dim = len(feature_fields) * embed_dim
#DNN layer
dnn_layers = []
input_dim = self.embedding_out_dim
self.mlp_dims = mlp_dims
for mlp_dim in mlp_dims:
# 全连接层
dnn_layers.append(nn.Linear(input_dim, mlp_dim))
dnn_layers.append(nn.BatchNorm1d(mlp_dim))
dnn_layers.append(nn.ReLU())
dnn_layers.append(nn.Dropout(p = dropout))
input_dim = mlp_dim
self.mlp = nn.Sequential(*dnn_layers)
# Corss Net layer
self.num_layers = num_layers
self.cross_w = nn.ModuleList([
nn.Linear(self.embedding_out_dim, 1, bias=False) for _ in range(num_layers)
])
self.cross_b = nn.ParameterList([
nn.Parameter(torch.zeros((self.embedding_out_dim,))) for _ in range(num_layers)
])
# LR layer
self.lr = nn.Linear(self.mlp_dims[-1]+self.embedding_out_dim, 1)
def forward(self, x):
tmp = x + x.new_tensor(self.offsets).unsqueeze(0)
# embeded dense vector
embeded_x = self.embedding(tmp).view(-1, self.embedding_out_dim)
# DNN out
mlp_part = self.mlp(embeded_x)
# Cross Net out
x0 = embeded_x
cross = embeded_x
for i in range(self.num_layers):
xw = self.cross_w[i](cross)
cross = x0 * xw + self.cross_b[i] + cross
# stack output
out = torch.cat([cross, mlp_part], dim = 1)
# LR out
out = self.lr(out)
out = torch.sigmoid(out.squeeze(1))
return out
7.DCN_v2
DCN-v2优化了DCN的cross layer,权重参数w由原来的vector变为方阵matrix,增加了网络层的表达能力;同时,为了保证线上应用的耗时不会因为cross layer参数量的增加而增加。观察到cross layer的matrix具有低秩性,使用矩阵分解,将方阵matrix转换为两个低维的矩阵、最后在低秩空间内,利用MoE多专家系统,对特征交叉做非线性变化,进一步增加对交叉特征的建模。直接上图,一目了然:
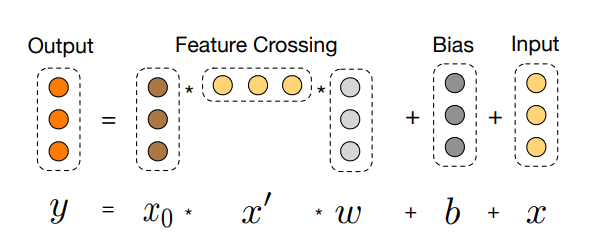
网络层权重参数由原来的vector w变为matrix W。DCN网络的cross layer的建模是element-wise;DCNv2 cross layer可以实现element-wise和feature-wise的特征交叉。但是这样直接转为矩阵,会极大增加计算量,且可能创新点太少?因此作者进行了相应的改进。
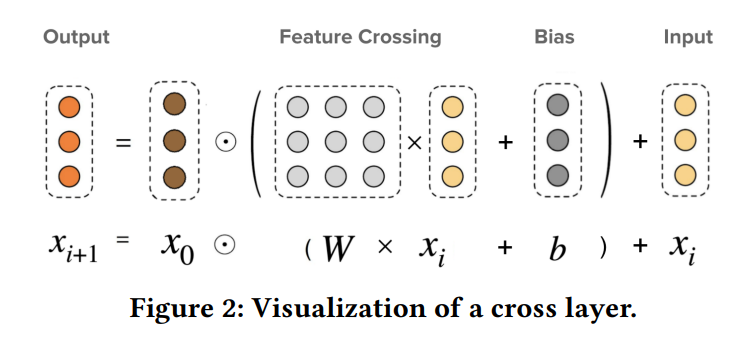
创新点一: 由于将特征embedding之后再拼接起来成了一个d维的向量,这个d太大了,而矩阵W维度是$d * d$ 。所有导致这个计算的复杂度就很高了,于是我们可以$W=UV^T$
,类似于矩阵分解的方法,将维度比较大的$d * d$ 矩阵分解成两个维度小一些的$d * r$矩阵。其中r r远小于d。这种方法叫做矩阵的低阶分解,和SVD有点类似。这也我们的交叉公式就发生了变化:
参数的数量和运算的复杂度都有效的变低了。
创新点二: 低维空间的交叉特征建模使得我们可以利用MoE。MoE由两部分组成:experts专家和gating门(一个关于输入x的函数)。我们可以使用多个专家,每个专家学习不同的交叉特征,最后通过gating将各个专家的学习结果整合起来,作为输出。这样就又能进一步增加对交叉特征的建模能力。
G是一个门函数,通常为sigmoid或者softmax。
改进的后模型据作者所说在降低了30%的复杂度的情况下,保留了模型的精度。附上核心代码:import numpy as np
import torch
import torch.nn as nn
class CrossNetMatrix(nn.Module):
"""
CrossNet of DCN-v2
"""
def __init__(self, in_features, layer_num=2):
super(CrossNetMatrix, self).__init__()
self.layer_num = layer_num
# Cross中的W参数 (layer_num, [W])
self.weights = nn.Parameter(torch.Tensor(self.layer_num, in_features, in_features))
# Cross中的b参数 (layer_num, [B])
self.bias = nn.Parameter(torch.Tensor(self.layer_num, in_features, 1))
# Init
for i in range(self.layer_num):
nn.init.xavier_normal_(self.weights[i])
for i in range(self.layer_num):
nn.init.zeros_(self.bias[i])
def forward(self, x):
"""
x : batch_size * in_features
"""
x0 = x.unsqueeze(2)
xl = x.unsqueeze(2)
for i in range(self.layer_num):
tmp = torch.matmul(self.weights[i], xl) + self.bias[i]
xl = x0 * tmp + xl
xl = xl.squeeze(2)
return xl
class CrossNetMix(nn.Module):
"""
CrossNet of DCN-V2 with Mixture of Low-rank Experts
公式如下:
G_i(xl) = Linear(xl)
E_i(xl) = x0·(Ul*g(Cl*g(Vl*xl)) + bl)
g() = tanh activate func
"""
def __init__(self, in_features, low_rank = 16, expert_num = 4, layer_num=2):
super(CrossNetMix, self).__init__()
self.layer_num = layer_num
self.expert_num = expert_num
# Cross中的U参数(layer_num, expert_num, in_features, low_rank)
self.U_params = nn.Parameter(torch.Tensor(layer_num, expert_num, in_features, low_rank))
# Cross中的V^T参数(layer_num, expert_num, low_rank, in_features)
self.V_params = nn.Parameter(torch.Tensor(layer_num, expert_num, low_rank, in_features))
# Cross中的C参数(layer_num, expert_num, low_rank, low_rank)
self.C_params = nn.Parameter(torch.Tensor(layer_num, expert_num, low_rank, low_rank))
# Cross中的bias(layer_num, in_features, 1)
self.bias = nn.Parameter(torch.Tensor(layer_num, in_features, 1))
# MOE 中的门控gate
self.gates = nn.ModuleList([nn.Linear(in_features, 1, bias=False) for i in range(expert_num)])
# Init
for i in range(self.layer_num):
nn.init.xavier_normal_(self.U_params[i])
nn.init.xavier_normal_(self.V_params[i])
nn.init.xavier_normal_(self.C_params[i])
for i in range(self.layer_num):
nn.init.zeros_(self.bias[i])
def forward(self, x):
"""
x : batch_size * in_features
"""
x0 = x.unsqueeze(2)
xl = x.unsqueeze(2)
for i in range(self.layer_num):
expert_outputs = []
gate_scores = []
for expert in range(self.expert_num):
# gate score : G(xl)
gate_scores.append(self.gates[expert](xl.squeeze(2)))
# cross part
# g(Vl·xl))
tmp = torch.tanh(torch.matmul(self.V_params[i][expert], xl))
# g(Cl·g(Vl·xl))
tmp = torch.tanh(torch.matmul(self.C_params[i][expert], tmp))
# Ul·g(Cl·g(Vl·xl)) + bl
tmp = torch.matmul(self.U_params[i][expert], tmp) + self.bias[i]
# E_i(xl) = x0·(Ul·g(Cl·g(Vl·xl)) + bl)
tmp = x0 * tmp
expert_outputs.append(tmp.squeeze(2))
expert_outputs = torch.stack(expert_outputs, 2) # batch * in_features * expert_num
gate_scores = torch.stack(gate_scores, 1) # batch * expert_num * 1
MOE_out = torch.matmul(expert_outputs, gate_scores.softmax(1))
xl = MOE_out + xl # batch * in_features * 1
xl = xl.squeeze(2)
return xl
class DeepCrossNetv2(nn.Module):
"""
Deep Cross Network V2
"""
def __init__(self, feature_fields, embed_dim, layer_num, mlp_dims, dropout = 0.1,
cross_method = 'Mix', model_method = 'parallel'):
"""
"""
super(DeepCrossNetv2, self).__init__()
self.feature_fields = feature_fields
self.offsets = np.array((0, *np.cumsum(feature_fields)[:-1]), dtype = np.long)
self.model_method = model_method
# Embedding layer
self.embedding = nn.Embedding(sum(feature_fields)+1, embed_dim)
torch.nn.init.xavier_uniform_(self.embedding.weight.data)
self.embedding_out_dim = len(feature_fields) * embed_dim
#DNN layer
dnn_layers = []
input_dim = self.embedding_out_dim
self.mlp_dims = mlp_dims
for mlp_dim in mlp_dims:
# 全连接层
dnn_layers.append(nn.Linear(input_dim, mlp_dim))
dnn_layers.append(nn.BatchNorm1d(mlp_dim))
dnn_layers.append(nn.ReLU())
dnn_layers.append(nn.Dropout(p = dropout))
input_dim = mlp_dim
self.mlp = nn.Sequential(*dnn_layers)
if cross_method == 'Mix':
self.CrossNet = CrossNetMix(in_features=self.embedding_out_dim)
elif cross_method == 'Matrix':
self.CrossNet = CrossNetMatrix(in_features=self.embedding_out_dim)
else:
raise NotImplementedError
# predict layer
if self.model_method == 'parallel':
self.fc = nn.Linear(self.mlp_dims[-1]+self.embedding_out_dim, 1)
elif self.model_method == 'stack':
self.fc = nn.Linear(self.mlp_dims[-1], 1)
else:
raise NotImplementedError
def forward(self, x):
tmp = x + x.new_tensor(self.offsets).unsqueeze(0)
# embeded dense vector
embeded_x = self.embedding(tmp).view(-1, self.embedding_out_dim)
if self.model_method == 'parallel':
# DNN out
mlp_part = self.mlp(embeded_x)
# Cross part
cross = self.CrossNet(embeded_x)
# stack output
out = torch.cat([cross, mlp_part], dim = 1)
elif self.model_method == 'stack':
# Cross part
cross = self.CrossNet(embeded_x)
# DNN out
out = self.mlp(cross)
# predict out
out = self.fc(out)
out = torch.sigmoid(out.squeeze(1))
return out
参考链接
[1] https://blog.csdn.net/weixin_44556141/article/details/120790057
[2] https://zhuanlan.zhihu.com/p/354994307
[3] https://blog.csdn.net/Jeremiah_/article/details/120740877
[4] https://zhuanlan.zhihu.com/p/361451464
[5] https://zhuanlan.zhihu.com/p/422141936
[6] https://zhuanlan.zhihu.com/p/138358291
